Ovaj klasičan zadatak o dodiru krugova zove se Apolonijev zadatak.
Primetimo da se ovaj zadatak može smatrati kao opšti zadatak, a ostale zadatke iz teorije dodira krugova možemo smatrati kao specijalne slučajeve ovog opšteg zadatka, kad se odgovarajući krug degeneriše u tačku ili u pravu, u zavisnosti od toga da li poluprečnik tog kruga teži ka nuli ili beskonačnosti.
Apolonijev zadatak je imao, kroz istoriju geometrije, niz različitih rešenja. Ovde navodimo Vietovo rešenje8.
Označimo poluprečnike datih krugova 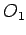 ,
, 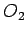 ,
, 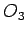 sa
sa 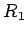 ,
, 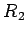 ,
, 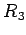 i pretpostavimo da je
i pretpostavimo da je
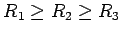 . Prvo razmotrimo slučaj kada su uslovi jednakosti izostavljeni i tada je
. Prvo razmotrimo slučaj kada su uslovi jednakosti izostavljeni i tada je 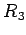 najmanji poluprečnik.
najmanji poluprečnik.
- Analiza: Analizirajmo slučaj kada se tri data kruga ne seku.
Iz centra kruga 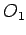 konstruišimo dva kruga: jedan
konstruišimo dva kruga: jedan 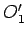 poluprečnika
poluprečnika 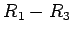 i drugi
i drugi 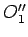 poluprečnika
poluprečnika 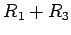 . Isto to uradimo iz centra
. Isto to uradimo iz centra 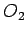 , tj. nacrtajmo krug
, tj. nacrtajmo krug 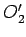 poluprečnika
poluprečnika 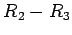 i
i 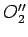 poluprečnika
poluprečnika 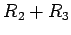 . Sad uzmimo u obzir centar kruga
. Sad uzmimo u obzir centar kruga 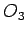 koji označimo sa A i postavimo zadatke određivanja kruga koji prolazi kroz tačku A i dodiruje dva kruga u ovim kombinacijama:
koji označimo sa A i postavimo zadatke određivanja kruga koji prolazi kroz tačku A i dodiruje dva kruga u ovim kombinacijama:
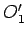
i
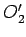
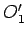
i
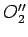
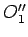
i
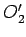
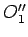
i
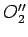
Svaki od tih zadataka spada u zadatak 8 (tačka i dva kruga). U opštem slučaju, takav zadatak može imati više rešenja, ali treba uzeti samo ono koje odgovara osnovnom postavljenom problemu.
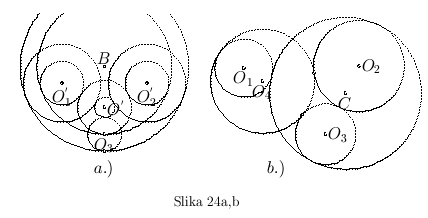
Slika 24.a pokazuje da takva dva kruga mogu biti: krug A koji dodiruje krugove 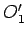 i
i 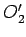 spolja i krug B koji obuhvata te krugove. Kada se krugu A smanji poluprečnik za
spolja i krug B koji obuhvata te krugove. Kada se krugu A smanji poluprečnik za 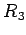 , onda će njemu koncentričan krug dodirivati spolja krugove
, onda će njemu koncentričan krug dodirivati spolja krugove 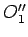 (to je veći krug sa centrom u
(to je veći krug sa centrom u 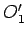 ),
), 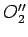 (veći krug sa centrom u
(veći krug sa centrom u 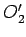 ) i
) i 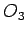 . Ako se krugu B poveća poluprečnik za
. Ako se krugu B poveća poluprečnik za 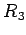 , on će dodirivati spolja krugove
, on će dodirivati spolja krugove 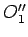 ,
, 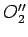 i
i 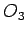 .
.
Na slici 24.b, na sličan način dobijamo: krug C koji dodiruje krug 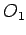 spolja, a krugove
spolja, a krugove 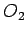 i
i 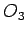 svojom unutrašnjom stranom, i krug D koji dodiruje krugove
svojom unutrašnjom stranom, i krug D koji dodiruje krugove 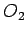 i
i 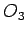 spolja i krug
spolja i krug 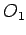 unutrašnjom stranom.
unutrašnjom stranom.
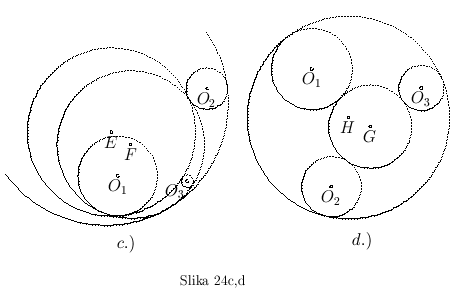
Na slici 24.c imamo: krug E koji dodiruje krugove 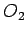 i
i 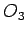 spolja i krug
spolja i krug 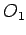 unutra, i krug F koji dodiruje krug
unutra, i krug F koji dodiruje krug 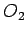 spolja i krugove
spolja i krugove 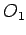 i
i 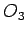 iznutra.
iznutra.
Na slici 24.d imamo: krug G koji dodiruje sva tri kruga 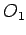 ,
, 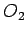 i
i 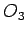 spolja, i krug H koji dodiruje sva tri kruga iznutra.
spolja, i krug H koji dodiruje sva tri kruga iznutra.
Prema tome, sve slučajeve možemo obuhvatiti sledećom tabelom:
| Pomoćni krugovi |
Rešenja |
Krugovi koje obuhvata traženi krug |
Krug kroz tačku treba |
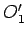 , , 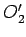 |
A |
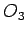 |
povećati |
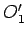 , , 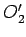 |
B |
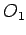 , , 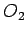 |
smanjiti |
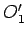 , , 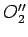 |
C |
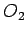 , , 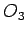 |
povećati |
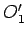 , , 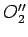 |
D |
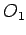 |
smanjiti |
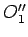 , , 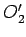 |
E |
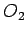 |
smanjiti |
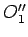 , , 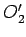 |
F |
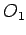 , , 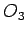 |
povećati |
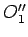 , , 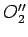 |
G |
- |
smanjiti |
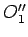 , , 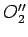 |
H |
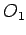 , , 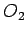 , , 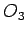 |
povećati |
Izvršena analiza pokazuje da, u opštem slučaju, kad se dati krugovi ne seku, zadatak ima osam rešenja.
- Konstrukcija: Iz izvršene analize zaključujemo da se ovaj problem se se može svesti na zadatak 8: naći krug koji dodiruje dva data kruga i prolazi kroz datu tačku. Ali, od četiri rešenja ovog zadatka, ovde se mogu koristiti samo dva.
- Dokaz: Dokaz konstrukcije ovog zadatka neposredno se svodi na dokaz zadatka 8 i na zaključak da krug koncentričan sa nađenim pomoćnim krugom, koji prolazi kroz datu tačku i dodiruje dva pomoćna kruga, treba konstruisati poluprečnikom povećanim za
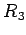 ili umanjenim za tu istu dužinu, u zavisnosti od toga kakve je prirode dodir sa pomoćnim krugovima koncentričnim sa krugovima
ili umanjenim za tu istu dužinu, u zavisnosti od toga kakve je prirode dodir sa pomoćnim krugovima koncentričnim sa krugovima 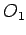 i
i 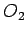 .
.
- Diskusija: Diskusija ovog zadatka za sve moguće položaje i veličine datih krugova je vrlo opširna. Navešćemo samo dva specijalna slučaja:
Prvi, kada dva kruga dodiruju jedan drugog, recimo spolja, a treći ima proizvoljan položaj. Od osam rešenja opšteg slučaja otpadaju dva slučaja, i to u zavisnosti od položaja trećeg kruga prema zajedničkoj tangenti krugova
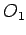 i
i 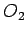 .
.
Drugi, kada se sva tri kruga nalaze u spoljašnjem dodiru. Tada imamo samo dva rešenja: krugove G i H, spoljašnjeg i unutrašnjeg dodira.
2005-04-12

