17.
Ako postoji ma koliko neprekidno proporcionalnih brojeva i krajnji su uzajamno prosti, onda se ne može prvi odnositi prema drugom kao poslednji prema ma kom drugom broju.
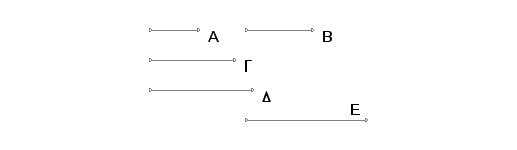
Neka postoji ma koliko neprekidno proporcionalnih brojeva A, B, G, D i krajnji od njih A i D su uzajamno prosti. Tvrdim da se ne može A odnositi prema B kao D prema ma kom drugom broju.
Zaista, ako je moguće, neka bude A prema B kao D prema E. Tada je, posle permutovanja, A prema D kao B prema E. Međutim, A i D su prosti, prosti i najmanji, a kako najmanji brojevi mere brojeve koji su sa njima u istoj razmeri isti broj puta, i to prethodni meri prethodni i naredni-naredni, znači A meri B. A pošto je A prema B kao B prema G, B meri G. Na ovaj način i A meri G. A pošto je B prema G kao G prema D, a B meri G, G meri D. Ali A meri G. Prema tome A meri i D, a meri i samo sebe. Dakle A meri A i D, koji su prosti, a to je nemoguće. Znači, ne može Biti A prema 3 ko 6 prema ma kom drugom broju. A to je trebalo dokazati.