19.
Za dva slična zapreminska broja postoje dva srednje proporcionalna broja; i razmera zapreminskog broja prema sličnom zapreminskom je tri put viša od razmera homologne ivice prema homolognoj ivici.
Neka su A i B dva zapreminska broja i ivice broja A - G, D, E, a ivice broja B - Z, H, Q. I pošto slični zapreminski brojevi imaju slične ivice, biće G prema D kao Z prema H, i D prema E kao H prema Q. Tvrdim, da za brojeve A i B postoje dva srednja proporcionalna broja i da je razmera A prema B tri puta viša od razmere G prema Z i Z prema H i E prema Q.
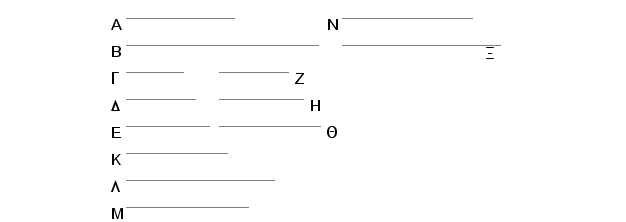
Zaista, neka G pomnoženo sa D proizvodi K, a Z pomnoženo sa H proizvodi L. Pošto su G i D u istoj razmeri sa Z i H, i od G i D je obrazovano K, a od Z i H je obrazovano L, to su K i L slični površinski brojevi, pa prema tome za K i L postoji jedan srednji proporcionalan broj. Neka to bude broj M. I neka je M proizvod D i Z, kako je to dokazano u prethodnoj teoremi. I pošto D pomnoženo sa G proizvodi K, a pomnoženo sa Z proizvodi M, biće G prema Z, kao K prema M. Ali, K je prema M kao M prema L. Prema tome su brojevi K, M i L neprekidno proporcionalni u razmeri G prema Z. I pošto je G prema D kao Z prema H, biće posle permutovanja, G prema Z kao D prema H. Iz istih razloga je i D prema H kao E prema Q. Na taj način su brojevi K, M, L neprekidno proporcionalni u razmeri G prema Z i D prema H i još E prema Q. Pa neka svako od E, Q pomnoženo sa M proizvodi N, odnosno X. A pošto je A zapreminski broj sa ivicama G, D, E to E pomnoženo proizvodom G i D proizvodi A. Ali je proizvod G i D jednak K, znači E pomnoženo sa K proizvodi A. Iz istih razloga i Q pomnoženo sa L proizvodi B. I pošto E pomnoženo sa K proizvodi A, a pomnoženo sa M proizvodi N, biće K prema M kao A prema N. A ako je K prema M kao G prema Z i kao D prema H još kao E prema Q, biće i G prema Z i D prema H i E prema Q, kao A prema N. Zatim, pošto svako od E i Q pomnoženo sa M proizvodi N, odnosno X, biće E prema Q kao N prema X. Ali je E prema Q kao G prema Z i kao D prema H. I prema tome je G prema Z i D prema H i E prema D kao A prema N i kao N prema X. Zatim, pošto Q pomnoženo sa M proizvodi X, ali i pomnoženo sa L proizvodi B, biće M prema L kao X prema B. Ali, M je prema L kao G prema Z i kao D prema H i kao E prema Q. I prema tome, kao što se odnosi G prema Z i D prema H i E prema Q, odnosi se ne samo X prema B, već i A prema N i N prema X. Na ovaj način su brojevi A, N, X, B neprekidno proporcionalni u razmeri navedenih ivica.
Tvrdim da je i razmera A prema B tri put viša od razmere homologne ivice prema homolognoj ivici, tj. od razmere broja G prema broju zvezdica Z ili D prema H ili još E prema Q. Zaista, pošto su brojevi A, N, X, B četiri neprekidno proporcionalna broja, biće razmera A prema B tri puta viša od razmere A prema N. Ali, kako je dokazano, A se odnosi prema N kao G prema Z i kao D prema H još kao E prema Q. Na ovaj način, razmera A prema B je tri put viša od razmere homolognih ivica, tj. od razmere broja G prema broju Z i D prema H i još E prema Q. A to je trebalo dokazati.