13.

Ako postoji proizvoljan broj neprekidno proporcionalnih brojeva i svaki takav broj pomnožen samim sobom proizvodi nešto (neki broj), onda su i dobijeni brojevi (kvadrati) neprekidno proporcionalni. Iako polazni brojevi, pomnoženi dobijenim, proizvode nešto (neke brojeve) onda su i tako dobijeni brojevi (kubovi) proporcionalni (to se isto produžuje i dalje).

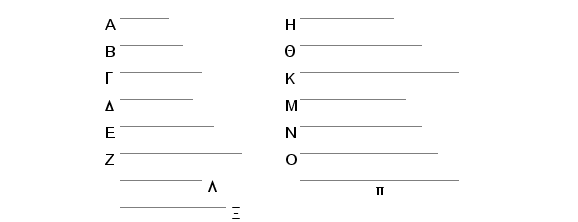
Neka su A, B, G, neki proizvoljno neprekidno proporcionalni brojevi, to znači da je A prema B kao B prema G i neka se od A, B, G pomnoženih samim sobom dobijaju brojevi D, E, Z, a od pomnoženih D, E, Z dobijaju brojevi H, Q, K. Tvrdim, da su brojevi D, E, Z i brojevi H, Q, K neprekidno proporcionalni.
Zaista, neka A pomnožena sa B proizvodi L, a svako od A i B pomnoženo sa L proizvodi M odnosno N. Zatim, B pomnoženo sa G proizvodi X, a svako od B i G pomnoženo sa X proizvodi O odnosno p.
Slično gore navedenom dokazuje se da su brojevi D, L, E i H, M, N, Q neprekidno proporcionalni sa razmerom A prema B i da su još i brojevi E, X, Z i Q, O, p, K neprekidno proporcionalni sa razmerom B prema G. I dalje, da je A prema B kao B prema G, te prema tome su i brojevi D, L, E u istoj razmeri kao i brojevi E, X, Z i još kao i brojevi H, M, N, Q prema brojevima Q, O, p i K. I količina brojeva D, L, E jednaka je količini brojeva E, X, Z. A i količina brojeva H, M, N, Q jednaka je količini brjeva Q, O, p, K, te je tada, prema jednakoj udaljenosti, D prema E, kao E prema Z i H prema Q, kao Q prema K. A to je trebalo dokazati.