34.

Za dva data broja naći najmanji broj koji oni mere.

Neka su data dva broja A, B. Treba naći najmanji broj koji oni mere.
Zaista, dva broja A i B ili su uzajamno prosti ili nisu. Neka, prvo, oni budu uzajamno prosti i neka A množeći B proizvodi G. Tada i B množeći A proizvodi G. Znači A i B mere broj G. Tvrdim da je G i najmanji broj koji oni mere. Ako nije, tada A i B mere neki broj koji je manji od G. Neka oni mere broj D. I koliko puta A meri D toliko neka bude jedinica u E, a koliko puta B meri D, toliko neka bude jedinica u Z. Prema tome A pomnoženo sa E proizvodi D, a B pomnoženo sa Z proizvodi D. Znači da je proizvod od A i E jednak proizvodu od B i Z. A to znači da A stoji prema B kao što Z stoji prema E. Međutim A i B su prosti, prosti i najmanji, ali najmanji mere brojeve koji su sa njima u istoj razmeri isti broj puta, veći meri veći i manji-manji. Prema tome B meri E, kao što naredni meri naredni. I pošt A posle množenja B i E proizvodi G i D, biće B prema E kao G prema D. I B meri E. Pa orema tome G meri D, veći broj meri manji, a to je nemoguće. Prema tome ne postoji broj manji od G, koji meri brojeve A i B. Na ovaj način broj G ja najmanji koji se meri brojevima A i B.

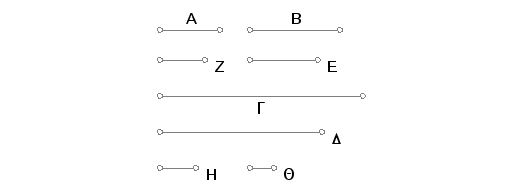
Neka sad brojevi A i B nisu uzajamno prosti i neka su Z i E najmanji brojevi koji su u istoj razmeri sa brojevima A i B. Tada je proizvod A i E jednak proizvodu B i Z. I neka A pomnoženo sa E proizvodi G. Ali tada i B pomnoženo sa Z proizvodi G. Prema tome A i B mere G. Tvrdim da je broj G najmanji broj koji oni mere. Ako nije, onda A i B mere neki broj koji je manji od G. Neka oni mere broj D. I, koliko puta A meri D, neka onoliko bude jedinica u H, a koliko puta B meri D neka bude jedinica u Q. Znači A pomnoženo sa H proizvodi D, a i B pomnoženo sa Q proizvodi D. Prema tome je proizvod od A i H jednak proizvodu od B i Q. Znači A se odnosi prema B kao Q prema H. Ali A se odnosi prema B kao Z prema E, pa i Z prema E kao Q prema H. I Z i E su najmanji, a najmanji mere isti broj puta brojeve koji su sa njima u istoj razmeri, veći meri veći i manji-manji. Prema tome E meri H. I pošto A množeći E i H proizvodi G i D biće E prema H kao G prema D. Ali E meri H, pa prema tome i G meri D, veći broj meri manji, a to je nemoguće. Dakle A i B ne mere broj koji je manji od G. Na ovaj način G je najmanji broj koji mere brojevi A i B. A to je trebalo dokazati.