26.
Ako su dva broja prosti u odnosu na dva druga broja, oba prema svakom od ovih, onda su i njihovi proizvodi uzajamno prosti.
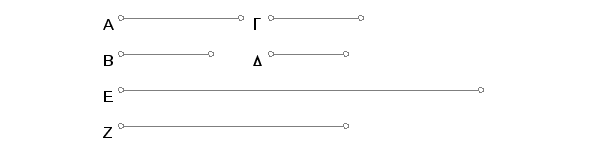
Ako su brojevi A i B u odnosu na dva broja G i D, ob prema svakom, prosti, i neka A množeći B proizvodi E, a G množeći D proizvodi Z. Tvrdim da su E i Z uzajamno prosti.
Zaista, pošto je svaki od brojeva A i B prost prema G, biće i proizvod od A i B prost prema G. A kako je proizvod od A i B broj E, biće i E i G uzajamno prosti. Iz istih razloga su uzajamno prosti i E i D. Prema tome je svaki od G i D prost prema E. To znači i proizvod od G i D je prost prema E. Ali proizvod od G i D je Z. Na ovaj način su E i Z uzajamno prosti. A to je trebalo dokazati.